 Model původního obrázku Kochańského z Acta Eruditorum ilustrující jeho přibližnou rektifikaci kružnice
Model původního obrázku Kochańského z Acta Eruditorum ilustrující jeho přibližnou rektifikaci kružnice
Kochańského konstrukce je přibližná metoda rektifikace kružnice neboli konstrukce úsečky o délce rovné polovině obvodu daného kruhu navržená v roce 1685 polským matematikem Adamem Adamandym Kochańským[1]. Umožňuje sestrojení úsečky, která je přibližně  -krát delší než daná úsečka. Jejím využitím lze také provést přibližnou kvadraturu kruhu.
-krát delší než daná úsečka. Jejím využitím lze také provést přibližnou kvadraturu kruhu.
Popis konstrukce
Je dána kružnice se středem v bodě  a poloměrem
a poloměrem 

- Sestrojíme průměr kružnice

- Sestrojíme tečnu ke kružnici v bodě

- Sestrojíme kružnici (nebo kruhový oblouk) se středem v bodě
 a poloměrem
a poloměrem  Jeden z průsečíků s původní kružnicí označíme
Jeden z průsečíků s původní kružnicí označíme 
- Sestrojíme kružnici (kruhový oblouk) se středem v bodě
 a poloměrem
a poloměrem  Jeden z průsečíků kruhových oblouků je
Jeden z průsečíků kruhových oblouků je  , druhý označíme
, druhý označíme  Body
Body  a
a  tvoří osu úsečky
tvoří osu úsečky 
- Průsečík
 s tečnou ke kružnici vedenou bodem
s tečnou ke kružnici vedenou bodem  označíme
označíme 
- Na polopřímku
 naneseme od bodu
naneseme od bodu  3krát vzdálenost
3krát vzdálenost  , čímž získáme postupně body
, čímž získáme postupně body 


- Úsečka
 má délku přibližně rovnou
má délku přibližně rovnou 

Stojí za zmínku, že úsečka  je výškou rovnostranného trojúhelníka
je výškou rovnostranného trojúhelníka  což znamená, že svírá úhel 30° s úsečkou
což znamená, že svírá úhel 30° s úsečkou  [2].
[2].
Odhad relativní chyby

Proto se chyba objeví až na pátém místě za desetinnou čárkou. Takové přiblížení v praktických případech obvykle postačuje.
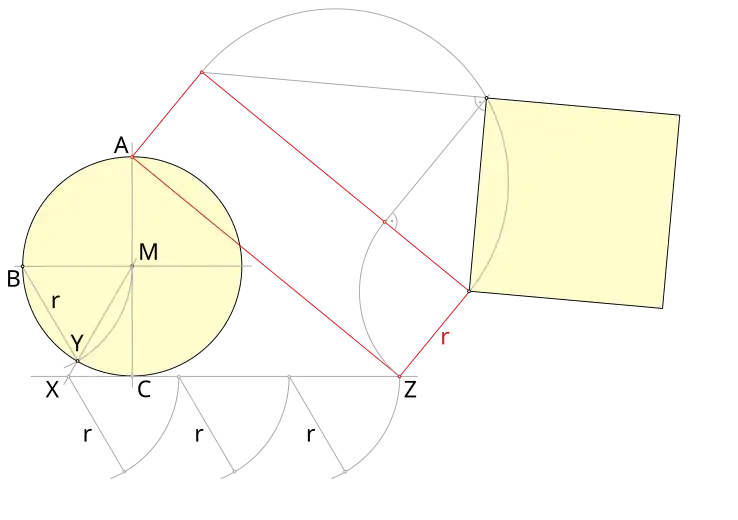
Kvadratura kruhu založená na Kochańského konstrukci
Na základě Kochańského konstrukce je možná také přibližná kvadratura kruhu. Ilustruje ji následující obrázek.
Odkazy
Reference
V tomto článku byl použit překlad textu z článku Konstrukcja Kochańskiego na polské Wikipedii.
- ↑ KOCHAŃSKI, Adam Adamandy. Observationes Cyclometricae ad facilitandam Praxin accomodatae. Acta Eruditorum. Roč. 1685, čís. 4, s. 394–398. (latinsky)
- ↑ BIELIŃSKI, Andrzej. Geometria wykreślna. Warszawa: [s.n.], 2005. ISBN 83-7207-564-6. (polsky)
Související články


