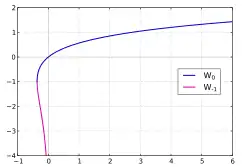
Graf funkce
W
0
(
x
)
{\displaystyle \color {blue}W_{0}(x)}
W
−
1
(
x
)
{\displaystyle \color {magenta}W_{-1}(x)}
z
=
R
e
(
W
0
(
x
+
i
y
)
)
{\displaystyle z=\mathrm {Re} (W_{0}(x+i\ y))}
reálná část funkce
W
0
{\displaystyle W_{0}}
z
=
I
m
(
W
0
(
x
+
i
y
)
)
{\displaystyle z=\mathrm {Im} (W_{0}(x+i\ y))}
imaginární část funkce
W
0
{\displaystyle W_{0}}
z
=
|
W
0
(
x
+
i
y
)
|
{\displaystyle z=|W_{0}(x+i\ y)|}
modul
W
0
{\displaystyle W_{0}}
Lambertova funkce W funkce používaná při řešení rovnic , které obsahují neznámou jak v základu, tak v exponentu . Nese jméno švýcarského učence Johanna Heinricha Lamberta . Je definována jako inverzní relace k funkci
f
(
w
)
=
w
e
w
,
{\displaystyle f(w)=we^{w},}
w
{\displaystyle w}
komplexních čísel , a značí se
W
(
z
)
.
{\displaystyle W(z).}
z
{\displaystyle z}
z
=
W
(
z
)
e
W
(
z
)
.
{\displaystyle z=W(z)e^{W(z)}.}
Protože funkce
f
{\displaystyle f}
prostá (injektivní) ,
W
(
z
)
{\displaystyle W(z)}
W
k
(
z
)
,
{\displaystyle W_{k}(z),}
k
∈
Z
{\displaystyle k\in \mathbb {Z} }
W
0
(
z
)
{\displaystyle W_{0}(z)}
(
−
1
/
e
,
0
)
{\displaystyle (-1/e,0)}
W
−
1
(
x
)
{\displaystyle W_{-1}(x)}
Vlastnosti
Rovnice
x
x
=
z
{\displaystyle x^{x}=z}
x
=
ln
(
z
)
W
(
ln
z
)
=
exp
W
(
ln
(
z
)
)
.
{\displaystyle x={\frac {\ln(z)}{W(\ln z)}}=\exp W(\ln(z)).}
Primitivní funkci k
W
{\displaystyle W}
integrováním substitucí : pokud
w
=
W
(
x
)
,
{\displaystyle w=W(x),}
x
=
w
e
w
.
{\displaystyle x=we^{w}.}
∫
W
(
x
)
d
x
=
x
(
W
(
x
)
−
1
+
1
W
(
x
)
)
+
C
.
{\displaystyle \int W(x)\ dx=x\left(W(x)-1+{\tfrac {1}{W(x)}}\right)+C.}
Derivace funkce
W
{\displaystyle W}
d
W
(
z
)
d
z
=
W
(
z
)
z
(
1
+
W
(
z
)
)
p
r
o
z
≠
−
1
e
.
{\displaystyle {\frac {dW(z)}{dz}}={\frac {W(z)}{z(1+W(z))}}\quad \mathrm {pro\ } z\neq -{\frac {1}{e}}.}
Důkaz
Derivováním rovnice
z
=
W
(
z
)
e
W
(
z
)
{\displaystyle z=W(z)e^{W(z)}}
z
{\displaystyle z}
1
=
W
(
z
)
e
W
(
z
)
W
′
(
z
)
+
W
′
(
z
)
e
W
(
z
)
=
W
′
(
z
)
(
W
(
z
)
e
W
(
z
)
+
e
W
(
z
)
)
,
{\displaystyle 1=W(z)e^{W(z)}W'(z)+W'(z)e^{W(z)}=W'(z)\left(W(z)e^{W(z)}+e^{W(z)}\right),}
W
′
(
z
)
=
1
z
+
e
W
(
z
)
=
W
(
z
)
W
(
z
)
z
+
W
(
z
)
e
W
(
z
)
=
W
(
z
)
z
(
W
(
z
)
+
1
)
.
{\displaystyle W'(z)={\frac {1}{z+e^{W(z)}}}={\frac {W(z)}{W(z)z+W(z)e^{W(z)}}}={\frac {W(z)}{z(W(z)+1)}}.}
Aplikace
Funkce
W
{\displaystyle W}
kombinatorice a při řešení diferenciálních rovnic . Pomocí této funkce lze dále vyřešit mnoho transcendentních rovnic zahrnujících mocninu neznámé, pokud je rovnici možné převést na tvar
Y
=
X
e
X
,
{\displaystyle Y=Xe^{X},}
Y
=
X
e
X
⟺
X
=
W
(
Y
)
.
{\displaystyle Y=Xe^{X}\;\Longleftrightarrow \;X=W(Y).}
Příklad 1
2
t
=
5
t
{\displaystyle 2^{t}=5t}
⇒
5
t
=
e
t
ln
2
{\displaystyle \Rightarrow 5t=e^{t\ln 2}}
⇒
1
5
t
=
e
−
t
ln
2
{\displaystyle \Rightarrow {\frac {1}{5t}}=e^{-t\ln 2}}
⇒
−
ln
2
5
⏟
Y
=
−
t
ln
2
⏟
X
e
−
t
ln
2
⏞
X
{\displaystyle \Rightarrow \underbrace {-{\tfrac {\ln 2}{5}}} _{Y}=\underbrace {-t\ln 2} _{X}e^{\overbrace {-t\ln 2} ^{X}}}
⇒
−
t
ln
2
⏟
X
=
W
(
−
ln
2
5
⏟
Y
)
{\displaystyle \Rightarrow \underbrace {-t\ln 2} _{X}=W{\Big (}\underbrace {-{\tfrac {\ln 2}{5}}} _{Y}{\Big )}}
⇒
t
=
−
W
(
−
ln
2
5
)
ln
2
{\displaystyle \Rightarrow t=-{\frac {W\left(-{\frac {\ln 2}{5}}\right)}{\ln 2}}}
Příklad 2
Nekonečné umocňování. Pokud hodnota
z
z
z
…
{\displaystyle z^{z^{z^{\ldots }}}}
c
=
z
z
z
…
,
{\displaystyle c=z^{z^{z^{\ldots }}},}
⇒
c
=
z
c
.
{\displaystyle \Rightarrow c=z^{c}.}
Z toho dostaneme:
c
=
−
W
(
−
ln
z
)
ln
z
.
{\displaystyle c=-{\frac {W\left(-\ln z\right)}{\ln z}}.}
Aby se dokázalo, že hodnota
z
z
z
…
{\displaystyle z^{z^{z^{\ldots }}}}
posloupnost
a
=
(
z
,
z
z
,
z
z
z
,
…
)
{\displaystyle a=(z,z^{z},z^{z^{z}},\dots )}
nebo (v rekurzivní formě):
{
a
1
=
z
a
n
=
z
a
n
−
1
{\displaystyle {\begin{cases}a_{1}=z\\a_{n}=z^{a_{n-1}}\end{cases}}}
a dokázat existenci limity . Pokud limita existuje, pak platí rovnost
lim
n
→
∞
a
n
=
c
.
{\displaystyle \lim \limits _{n\to \infty }a_{n}=c.}
Příklad 3
Diferenciální rovnice vyjadřující opožděnou reakci
y
′
(
t
)
=
a
y
(
t
−
1
)
{\displaystyle y'(t)=ay(t-1)}
má charakteristickou rovnici
λ
=
a
e
−
λ
,
{\displaystyle \lambda =ae^{-\lambda },}
λ
=
W
k
(
a
)
,
{\displaystyle \lambda =W_{k}(a),}
k
{\displaystyle k}
a
{\displaystyle a}
reálné , stačí vzít v úvahu větev
W
0
(
a
)
{\displaystyle W_{0}(a)}
y
(
t
)
=
e
W
k
(
a
)
t
.
{\displaystyle y(t)=e^{W_{k}(a)\,t}.}
Vybrané hodnoty
W
0
(
−
π
2
)
{\displaystyle W_{0}(-{\tfrac {\pi }{2}})}
=
π
2
i
{\displaystyle ={\tfrac {\pi }{2}}i}
W
0
(
−
1
)
{\displaystyle W_{0}(-1)}
≈
−
0,318
13
+
1,337
23
i
{\displaystyle \approx -0{,}31813+1{,}33723i}
W
0
(
−
1
e
)
{\displaystyle W_{0}(-{\tfrac {1}{e}})}
=
−
1
{\displaystyle =-1}
W
0
(
−
ln
2
2
)
{\displaystyle W_{0}(-{\tfrac {\ln 2}{2}})}
=
−
ln
2
{\displaystyle =-\ln 2}
W
0
(
0
)
{\displaystyle W_{0}(0)}
=
0
{\displaystyle =0}
W
0
(
e
)
{\displaystyle W_{0}(e)}
=
1
{\displaystyle =1}
W
0
(
1
)
{\displaystyle W_{0}(1)}
=
Ω
≈
0,567
14329
{\displaystyle =\Omega \approx 0{,}56714329}
Reference
V tomto článku byl použit překlad textu z článku Funkcja W Lamberta
Literatura
Oleszkiewicz Krzysztof, Funkcja Lamberta, „Delta”, 2014, ISSN 0137-3005 (polsky)
Externí odkazy
Obrázky, zvuky či videa k tématu Lambertova W funkce
Portály: Matematika


![]() Obrázky, zvuky či videa k tématu Lambertova W funkce na Wikimedia Commons
Obrázky, zvuky či videa k tématu Lambertova W funkce na Wikimedia Commons