Mocninná funkce

Mocninná funkce je elementární matematická funkce, jejíž hodnoty jsou přímo úměrné určité mocnině proměnné.

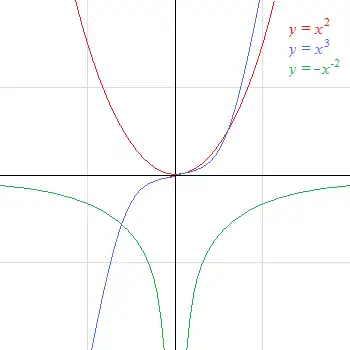
Mocninná funkce s reálným exponentem r je funkce ve tvaru:

${\displaystyle f\colon x\mapsto ax^{r}=ae^{r\ln x}\qquad a,r\in \mathbb {R} ,}$

kde ${\displaystyle a\neq 0}$ a ${\displaystyle r\neq 0}$ jsou konstanty a ${\displaystyle x>0}$ je proměnná.

Mocninná funkce s racionálním exponentem je funkce ve tvaru:

${\displaystyle f\colon x\mapsto ax^{\frac {n}{m}}=a{\sqrt[{m}]{x^{n}}}\qquad a\in \mathbb {R} ,}$

kde ${\displaystyle a\neq 0}$ je konstanta, ${\displaystyle n\in \mathbb {Z} -\{0\}}$, ${\displaystyle m\in \mathbb {N} }$ a ${\displaystyle x>0}$ je proměnná.

Mocninná funkce s celočíselným exponentem je polynomiální funkce s nejvýše jedním nenulovým koeficientem. Speciální případy pro ${\displaystyle n\neq 0}$:

Sudá mocninná funkce

${\displaystyle f\colon x\mapsto x^{2n}\qquad n\in \mathbb {N} }$, normální parabola otevřená nahoru

${\displaystyle f\colon x\mapsto -x^{2n}\qquad n\in \mathbb {N} }$, normální parabola otevřená dolu

${\displaystyle f\colon x\mapsto x^{-2n}\qquad n\in \mathbb {N} }$, hyperbola v prvním a druhém kvadrantu (${\displaystyle x\neq 0}$)

${\displaystyle f\colon x\mapsto -x^{-2n}\qquad n\in \mathbb {N} ,}$, hyperbola v třetím a čtvrtém kvadrantu (${\displaystyle x\neq 0}$)

Lichá mocninná funkce

${\displaystyle f\colon x\mapsto x^{2n+1}\qquad n\in \mathbb {N} }$, normální parabola v prvním a třetím kvadrantu

${\displaystyle f\colon x\mapsto -x^{2n+1}\qquad n\in \mathbb {N} }$, normální parabola v druhém a čtvrtém kvadrantu

${\displaystyle f\colon x\mapsto x^{-(2n+1)}\qquad n\in \mathbb {N} }$, hyperbola v prvním a třetím kvadrantu (${\displaystyle x\neq 0}$)

${\displaystyle f\colon x\mapsto -x^{-(2n+1)}\qquad n\in \mathbb {N} }$, hyperbola v druhém a čtvrtém kvadrantu (${\displaystyle x\neq 0}$)

a pro ${\displaystyle n=0}$:

${\displaystyle f\colon x\mapsto x^{-1}\qquad }$ rovnoosá hyperbola v prvním a třetím kvadrantu (${\displaystyle x\neq 0}$)

${\displaystyle f\colon x\mapsto -x^{-1}\qquad }$ rovnoosá hyperbola v druhém a čtvrtém kvadrantu (${\displaystyle x\neq 0}$)

Definiční obor závisí na exponentu ${\displaystyle r}$, konkrétně na jeho celočíselnosti (tj. zda ${\displaystyle r\in \mathbb {Z} }$) a znaménku podle následující tabulky.

	${\displaystyle r>0}$	${\displaystyle r<0}$	${\displaystyle r=0}$
${\displaystyle r\in \mathbb {Z} }$	${\displaystyle \mathbb {R} }$	${\displaystyle \mathbb {R} \setminus \{0\}}$	${\displaystyle \mathbb {R} \setminus \{0\}}$ nebo ${\displaystyle \mathbb {R} }$[pozn. 1]
${\displaystyle r\notin \mathbb {Z} }$	${\displaystyle \mathbb {R} _{0}^{+}}$	${\displaystyle \mathbb {R} ^{+}}$	—

Obor hodnot závisí na konstantě ${\displaystyle a}$ a exponentu ${\displaystyle r}$.

	${\displaystyle r>0}$		${\displaystyle r<0}$		${\displaystyle r=0}$
	${\displaystyle r}$ sudé nebo ${\displaystyle \notin \mathbb {Z} }$	${\displaystyle r}$ liché	${\displaystyle r}$ sudé nebo ${\displaystyle \notin \mathbb {Z} }$	${\displaystyle r}$ liché
${\displaystyle a>0}$	${\displaystyle \mathbb {R} _{0}^{+}}$	${\displaystyle \mathbb {R} }$	${\displaystyle \mathbb {R} ^{+}}$	${\displaystyle \mathbb {R} \setminus \{0\}}$	${\displaystyle \{a\}}$
${\displaystyle a<0}$	${\displaystyle \mathbb {R} _{0}^{-}}$	${\displaystyle \mathbb {R} }$	${\displaystyle \mathbb {R} ^{-}}$	${\displaystyle \mathbb {R} \setminus \{0\}}$
${\displaystyle a=0}$	${\displaystyle \{0\}}$

• BARTSCH, Hans-Jochen. Matematické vzorce. 4. vyd. Praha: Academia, 1994. 832 s. ISBN 80-200-1448-9. 

• Obrázky, zvuky či videa k tématu mocninná funkce na Wikimedia Commons
• https://www2.karlin.mff.cuni.cz/~portal/funkce/?page=mocninne