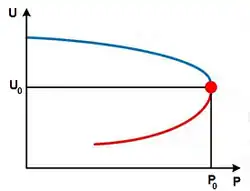
Nosová křivka (stabilita napětí)

Nosová křivka popisuje vztah mezi činným výkonem dodávaným do elektrické zátěže a napětím na zátěži v energetické elektrizační soustavě za konstantního účiníku.^[1] Název křivky je dán tvarem připomínající lidský nos.^[2] Celkový tvar křivky (podobný parabole položené na boku) je definován základními elektrickými rovnicemi. Křivka je důležitá pro analýzu stability napětí, protože souřadnice "špičky nosu" definují maximální výkon, který můžeme vedením přenést.

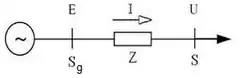
Předpokládejme harmonické symetrické zatížení třífázového vedení, modelovaného danou impedancí ${\displaystyle \mathbf {Z} }$, napájeného zdrojem udržujícím stálé harmonické napětí v napájecím bodě, pak dle 2. Kirchhoffova zákona pro fázory sdružených napětí ${\displaystyle \mathbf {E} }$ a ${\displaystyle \mathbf {U} }$ a fázor proudu ${\displaystyle \mathbf {I} }$ platí:

${\displaystyle \mathbf {E} -\mathbf {U} ={\sqrt {3}}\mathbf {\ Z\ I} }$

a po roznásobení výše uvedené rovnice činitelem ${\displaystyle {\sqrt {3}}\mathbf {I} ^{\mathbf {*} }}$ dostaneme výkonovou bilanci:

${\displaystyle \mathbf {S} _{g}-\mathbf {S} =3\mathbf {\ Z\ } I^{2}}$

tj.:

${\displaystyle \left|\mathbf {S} _{g}-\mathbf {S} \right|=3\mathbf {\ } \left|\mathbf {Z} \right|\mathbf {\ } I^{2}}$

tj. pro ${\displaystyle Z^{2}=R^{2}+X^{2}}$ a ${\displaystyle S^{2}=P^{2}+Q^{2}}$ po povýšení obou stran výše uvedené rovnice na druhou dostaneme:

${\displaystyle S_{g}^{2}-S^{2}-2(3I^{2}(RP+XQ))=\left(3I^{2}\right)^{2}Z^{2}}$

a po roznásobení výše uvedené rovnice převrácenou hodnotou činitele ${\displaystyle 3I^{2}}$ dostaneme:

${\displaystyle E^{2}-U^{2}-2(RP+XQ)=Z^{2}{\frac {S^{2}}{U^{2}}}}$

a po dalším roznásobení výše uvedené rovnice činitelem ${\displaystyle -U^{2}}$ dostaneme tzv. nosovou křivku:

${\displaystyle U^{4}-2\ ({\frac {1}{2}}E^{2}-(RP+XQ))\ U^{2}=-Z^{2}S^{2}}$

tj. pro ${\displaystyle \alpha ={\frac {1}{2}}E^{2}-(RP+XQ)}$ a ${\displaystyle \beta =Z^{2}S^{2}}$ dostaneme:

${\displaystyle f(U)\equiv U^{4}-2\alpha \ U^{2}+\beta =0}$

tj.:

${\displaystyle U^{4}-2\alpha \ U^{2}+\alpha ^{2}-\alpha ^{2}+\beta =0}$

tj.:

${\displaystyle \left(U^{2}-\alpha \right)^{2}=\alpha ^{2}-\beta }$

Položením derivace funkce ${\displaystyle f}$ nule určíme napětí ${\displaystyle U_{0}}$, v kterém funkce nabývá maxima ${\displaystyle P_{0}}$:

${\displaystyle {\frac {df}{dU}}=4U^{3}-4\alpha \ U=0\ \ \ \ \ \Rightarrow \ \ \ \ \ U_{0}^{2}=\alpha }$

pro které platí:

${\displaystyle \alpha ^{2}-2\alpha ^{2}+\ \beta =0\ \ \ \ \ \Rightarrow \ \ \ \ \ \alpha ^{2}=\beta }$

tj.:

${\displaystyle {\frac {1}{4}}E^{4}-E^{2}\left(RP_{0}+XQ_{0}\right)+\left(RP_{0}+XQ_{0}\right)^{2}=\left(R^{2}+X^{2}\right)\left(P_{0}^{2}+Q_{0}^{2}\right)}$

tj.:

${\displaystyle {\frac {1}{4}}E^{4}-E^{2}\left(RP_{0}+XQ_{0}\right)+R^{2}P_{0}^{2}+2RP_{0}XQ_{0}+X^{2}Q_{0}^{2}=R^{2}P_{0}^{2}+X^{2}P_{0}^{2}+R^{2}Q_{0}^{2}+X^{2}Q_{0}^{2}}$

tj.:

${\displaystyle {\frac {1}{4}}E^{4}-E^{2}\left(RP_{0}+XQ_{0}\right)=X^{2}P_{0}^{2}-2RP_{0}XQ_{0}+R^{2}Q_{0}^{2}=\left(XP_{0}-RQ_{0}\right)^{2}}$

tj. pro ${\displaystyle P_{0}\neq 0}$ a účiník ${\displaystyle \cos \varphi }$:

${\displaystyle (X-R\ tg\varphi )^{2}P_{0}^{2}+E^{2}(R+X\ tg\varphi )P_{0}-{\frac {1}{4}}E^{4}=0}$

Dále určíme diskriminant výše uvedené kvadratické rovnice o parametrech ${\displaystyle R,X,E,\varphi }$:

${\displaystyle D=E^{4}(R+Xtg\varphi )^{2}+(X-R\ tg\varphi )^{2}E^{4}=E^{4}Z^{2}\left(1+{tg}^{2}\varphi \right)={\frac {E^{4}Z^{2}}{\cos ^{2}\varphi }}>0}$

a její kořeny:

${\displaystyle P_{01}={\frac {-E^{2}(R+Xtg\varphi )+{\frac {E^{2}Z}{cos\varphi }}}{2(X-R\ tg\varphi )^{2}}}={\frac {E^{2}(Z\ -(Rcos\varphi +Xsin\varphi ))}{2(Xcos\varphi -R\ sin\varphi )^{2}}}cos\varphi >0}$

${\displaystyle P_{02}={\frac {-E^{2}(R+Xtg\varphi )-{\frac {E^{2}Z}{cos\varphi }}}{2(X-R\ tg\varphi )^{2}}}=-{\frac {E^{2}(Z+(Rcos\varphi +Xsin\varphi ))}{2(Xcos\varphi -R\ sin\varphi )^{2}}}cos\varphi <0}$

jejichž vyjádření dává smysl při splnění následujících tří podmínek:

${\displaystyle \varphi \in (-{\frac {\pi }{2}},{\frac {\pi }{2}})\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ PX\neq QR\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ Z\ \pm (Rcos\varphi +Xsin\varphi )>0}$

přičemž druhý kořen nemá smysl uvažovat, pak limitní pracovní bod ${\displaystyle \left\lbrack P_{0},U_{0}\right\rbrack }$ určíme následovně:

${\displaystyle P_{0}={\frac {E^{2}(Z\ -(Rcos\varphi +Xsin\varphi ))}{2(Xcos\varphi -R\ sin\varphi )^{2}}}cos\varphi \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ U_{0}^{2}={\frac {Z\ P_{0}}{\cos \varphi }}}$

tj. uvažujeme-li pouze činnou zátěž při zanedbání odporu, tj. ${\displaystyle \varphi =0}$ a ${\displaystyle R=0}$, dostaneme limitní pracovní bod ve tvaru:

${\displaystyle P_{0}={\frac {E^{2}}{2X}}={\frac {U_{0}^{2}}{X}}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ U_{0}={\sqrt {X\ P_{0}}}={\frac {E}{\sqrt {2}}}}$

Z výše uvedeného plyne, že pohybuje-li se pracovní bod s rostoucím zatížením vedení zleva doprava po modré části nosové křivky, tak je napětí na konci vedení stabilní, překročí-li však pracovní bod svou limitní pozici, pak se bude pohybovat s klesajícím zatížením vedení zprava doleva po červené části nosové křivky při současném kolapsu napětí na konci vedení (viz obrázek).

Uvažujeme-li ${\displaystyle PX=QR}$, pak nám výše uvedená kvadratická rovnice přejde za podmínky ${\displaystyle R,X>0}$ do lineárního tvaru:

${\displaystyle (X-X)^{2}P_{0}^{2}+E^{2}(R+X{\frac {X}{R}})\ P_{0}-{\frac {1}{4}}E^{4}=0}$

tj.:

${\displaystyle {\frac {Z^{2}}{R}}P_{0}={\frac {1}{4}}E^{2}\ \ \ \ \ \Rightarrow \ \ \ \ \ P_{0}=R\ \left({\frac {E}{2\ Z}}\right)^{2}\ \ \ \ \ \Rightarrow \ \ \ \ \ U_{0}={\frac {E}{2\ }}}$

kde:

${\displaystyle U_{0}^{2}={\frac {Z\ P_{0}}{\cos \varphi }}={\sqrt {\left(1+{tg}^{2}\varphi \right)}}\ Z\ R\ \left({\frac {E}{2\ Z}}\right)^{2}=\left({\frac {E}{2\ }}\right)^{2}\ \ \ \ \ \ \ \ \ \ {\sqrt {\left(1+{tg}^{2}\varphi \right)}}={\frac {Z}{R}}}$

• Elektrická síť
• Elektrické napětí
• Elektrický výkon

• Miloš Křivan: Matematický model elektrické sı́tě