Paradox dvojčat

Paradox dvojčat je fyzikální myšlenkový experiment zaměřený na problematiku dilatace času v Einsteinově teorii relativity.

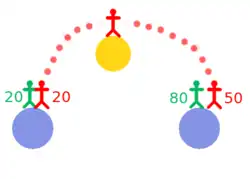
Jsou dva bratři – dvojčata, z nichž jeden cestuje raketou k sousední hvězdě. Po návratu zjistí, že jeho bratr, který zůstal na Zemi, zestárl mnohem více než on sám. Protože se raketa pohybovala rychlostí srovnatelnou s rychlostí světla, plynul čas na její palubě výrazně pomaleji ve srovnání s plynutím času na Zemi. Paradoxem se označuje kvůli možné chybné úvaze, že lze pohyb považovat za relativní a očekávat, že bratr na Zemi zestárnul naopak méně, protože se (i s planetou Zemí) pohyboval vysokou rychlostí on, vzhledem k druhému bratrovi v raketě.

Autorem paradoxu publikovaného roku 1911 je Paul Langevin, propagátor Einsteinovy teorie ve Francii. V té době speciální teorii relativity přednášel na Collège de France, kam roku 1922 přijel na jeho pozvání přednášet sám Einstein. Původní myšlenkový experiment Langevinova střela obsahoval jen cestovatele, který cestoval v projektilu, ve kterém byl na svou pouť vystřelen a který byl převzat ze známého Verneova románu Ze Země na Měsíc. Teprve jeho rozšířením o dvojče vznikl charakter paradoxu.

Původně tedy byl problém řešen jen v rámci inerciálních soustav, protože nad zapojením gravitace a zrychlení do relativity Einstein teprve bádal. Obecnou teorii relativity publikoval až roku 1915 a uznána byla roku 1919. Umožnila další přístupy a varianty řešení a také do úlohy přinesla další faktory zapříčiňující dilataci času jako je gravitace a rotace Země.

Teoretické propočty, jaké se řeší v rámci myšlenkového experimentu, byly ověřeny reálným Hafeleovým–Keatingovým experimentem roku 1971. Praktické každodenní uplatnění mají u satelitních navigací, protože bez započtení časové dilatace navigační družice (jejích hodin) oproti pozemskému uživateli by nebylo možné určovat polohu.

Paradox vzniká v důsledku domnělé symetrie. Z pohledu vesmírného bratra se pohybuje Země i s jeho bratrem, pomaleji by tedy měl plynout čas na Zemi. Na Zem by se tedy vesmírný bratr měl vrátit starší. Jak tento paradox vysvětlit?

Vysvětlení je, že časová dilatace platí dle speciální teorie relativity pro inerciální soustavy, tedy soustavy, které jsou v klidu nebo se pohybují rovnoměrným přímočarým pohybem. To neplatí o raketě, která se pohybuje nejdříve směrem od Země a pak změní směr letu a vrací se, vesmírný bratr tedy není inerciálním pozorovatelem. Raketa nemění směr letu jen relativně k Zemi, ale i vzhledem ke směru své předchozí cesty. Cestující dvojče tedy musí provést nějaký druh otočky, aktivní manévr, který způsobí změnu relativního pohybu (místo oddalování přibližování dvojčat). Symetrie se touto otočkou poruší a cestující dvojče skutečně zestárne méně než to na Zemi.^[1][2]

Symetrie zůstane zachována, pokud se bude uvažovat jen cesta jedním směrem. Je to důsledek relativnosti současnosti, protože neexistuje absolutní čas, podle kterého by bylo možno určit, jakou událost prožíval pozemský bratr v okamžiku, kdy bratr v raketě dosáhl vzdálené hvězdy. Čas záleží na pozorovateli a zvolené soustavě, pro každého z bratrů bude jiná pozemská současnost pro okamžik dosažení hvězdy raketou. Podobně nelze určit, kdo z dvojčat víc zestárnul, zda dříve oslavil třicáté narozeniny pozemský bratr, nebo bratr v raketě. Obě události (oboje narozeniny) nastanou pro každého z bratrů v jiném pořadí.

V klasickém zadání jeden z bratrů zůstává na planetě Zemi. Ta však není v klidu, ale v nepřímočarém pohybu a na jejím povrchu je plynutí času ovlivňováno různými relativistickými faktory, např. gravitačním působením Země. Vhodnější je proto umístit dvojče do kosmické stanice ve Sluneční soustavě, pak jeho vztažnou soustavu lze považovat za nehybnou a jeho plynutí času za neovlivněné.

Některé varianty nepočítají se zrychlením, tedy že raketa musí zrychlovat a brzdit (záporné zrychlení). Počítá se s tím, že raketa letí rovnoměrným přímočarým pohybem tam i zpět. Protože reálně by nebylo možné zrychlení zanedbat, existují upravená zadání bez fyzicky cestujícího bratra a se dvěma raketami předávající si naměřené časy. První raketa při míjení Země synchronizuje svůj čas s pozemským časem, u vzdálené hvězdy předá naměřený čas raketě letící opačným směrem, ta pak při míjení Země odešle součet naměřených časů k porovnání s pozemským časem. Případně pro názornost si lze představit, že jedno dvojče cestu absolvuje pomocí teleportace při výměně časů.

Takto formulované zadání zahrnuje tři inerciální soustavy, které umožňují řešení pomocí jednodušší speciální teorie relativity. Podle ní, pokud se dvě soustavy vůči sobě pohybují, každý pozorovatel vnímá plynutí času toho druhého jako pomalejší. A skutečně, posádky obou raket během cesty mezi Sluneční soustavou a blízkou hvězdou na svých hodinách naměřily více času, než během těchto dob uběhlo nehybnému dvojčeti ve Sluneční soustavě. Zdá se tedy, že součet časů z raket je delší než součet odpovídajících časů nehybného dvojčete a to by tedy mělo mladší.

Důvodem paradoxu je relativita současnosti. V okamžiku, kdy se obě rakety míjejí, posádce vzdalující se rakety odpovídá jeden bod v životě nehybného dvojčete, zatímco posádce přibližující se rakety odpovídá mnohem pozdější bod v jeho životě. Jinak řečeno, část života nehybného dvojčete odpovídá současnosti raket za místem míjení, pro vzdalující se raketu probíhá až po bodu setkání, pro přibližující se raketu to byla současnost před okamžikem setkání, proto tento čas není započítán do časů letu tam a zpět. Tedy cestující dvojče, které se při míjení raket teleportuje, „přeskočí“ současnost tohoto bratrova období, které je tak dlouhé, že se cestující dvojče vrátí mladší než jeho nehybný bratr.

V Minkowského diagramu (obrázek výše) jsou odlišné současnosti vyznačené jako jinak skloněné roviny. Cestující dvojče v okamžiku otočky mění rovinu současnosti (z modré na červenou) a tím dojde ke zkrácení jeho času a zestárne méně než jeho dvojče. To zůstalo nehybné, neprošlo podobnou změnou, a proto platí dle speciální relativity, že jeho čas probíhal rychleji než jeho bratra, tedy oproti svému sourozenci zestárl.

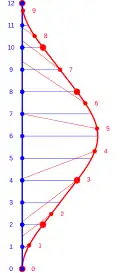
„Skok“ však není reálný, pokud si budou dvojčata posílat pravidelné světelné signály, všechny k protějšku dorazí se zpožděním daným jejich aktuální vzdáleností a nevznikne ani žádné hluché období. Na druhém obrázku každé dvojče vysílá jednou za rok světelný signál, který tak nese informaci o jeho věku. První signály oba přijmou po dvou letech, druhé signály po čtyřech letech. Tato symetrie je narušena otočkou lodi: pozemské dvojče na další dva signály vyslané ještě ze vzdalující se lodi čeká dva a čtyři roky (červené šipky), přibližující se loď už přijímá signály naopak častěji (s vyšší frekvencí, modré šipky). Celkově tedy pozemské dvojče stihne vyslat více signálů než jeho sourozenec, který stárne pomaleji. V diagramu je zestárnutí o 10 a 8 let. Barvy šipek označují relativistický Dopplerův jev (červený a modrý posuv vlnové délky světla) podle směru letu, obě barvy u bodu obratu mohou např. zastupovat dvojici míjejících se raket (viz výše).

Realističtější varianta počítá s tím, že raketa konstatně zrychluje (zrychlení a), až dosáhne v půlce cesty tam maximální rychlost a začne stejně intenzivně brzdit (zrychlení -a), až zastaví v cíli; stejný postup použije pro cestu zpět. Celý let tedy bude mít čtyři stejně dlouhé fáze: zrychlování, zpomalování, zrycholvání opačným směrem, zpomalování. Raketa tedy po celou dobu letu bude podléhat zrychlení o konstantní velikosti a, měnit se bude jen směr působení (směr tahu motoru rakety), vždy přesně uprostřed mezi oběma cíly.

Pokud se zvolí velikost zrychlení a = 1 G (tíhové zrychlení Země), bude dvojče pohodlně cestovat s efektem umělé gravitace a během několika let skutečně doletí k nejbližší hvězdě. Reálně však takové cestě brání to, že pohon takové rakety je zcela mimo možnosti lidstva, protože permanentní akcelerace by spotřebovávala obrovské množství energie.

Řešení na poli speciální teorie relativity již neumožňuje porovnávat soustavy, protože raketa se pohybuje nerovnoměrným pohybem. Je však jako základ soustavy možnost zvolit nehybné dvojče (Sluneční soustavu) a matematicky popsat cestu druhého dvojčete. Výpočty jsou to netriviální, protože jejich součástí je proměnlivá rychlost rakety. Ta vstupuje do vzorce pro rozdíl časů obou dvojčat dle speciální relativity, ale také do výpočtu dráhy a rychlosti rakety. Ty jsou totiž ovlivněny hmotností rakety, která dle speciální relativity roste s její rychlostí.

Poznatky plynoucí z obecné teorie relativity umožňují jiné řešení tohoto zadání. Ta je založena na Einsteinově principu ekvivalence gravitace a zrychlení, tedy že zrychlení a gravitace mají stejné důsledky. To je ilustrováno známým příkladem právě rakety o zrychlení G, která má na cestovatele stejný efekt jako nehybný pobyt v gravitačním poli G.

Podle obecné relativity je cestující dvojče vystaveno konstantnímu zrychlení a tedy dochází k dilataci (zpomalení) času stejnému, jako by se nacházelo v odpovídajícím gravitačním poli, a jeho čas tedy plyne pomaleji než dvojčeti v nehybné kosmické stanici ve Sluneční soustavě. Výpočet se stejnými parametry vede ke stejnému výsledku rozdílů časů jako složitější výpočty z pozic speciální relativity.

Na internetu mezi laiky kolují různá nesprávná a nepřesná řešení paradoxu dvojčat.^[3]

• Jednoduchý případ je řešení ignorující narušení symetrie změnou inerciální soustavy rakety při změně směru letu, které dochází k závěru, že dilatace je symetrická a dvojčata při shledání budou stejně stará.
• Naopak řešení ignorující symetrii předpokládá, že když dvojče u vzdálené hvězdy odešle svůj věk a pozemské dvojče v okamžiku, kdy se bratr nachází u hvězdy, zaznamená svůj věk, dodatečním porovnáním údajů lze zjistit, že cestující dvojče stárne pomaleji už před otočkou. Okamžik průletu se určuje dle pozemské soustavy, když ji zaměníme za soustavu rakety, bude mladší pozemské dvojče a symetrie je zachována (současnost je relativní).
• Další nesprávné řešení odvozuje dilataci času od Dopplerova jevu. Pomalejší stárnutí je odvozováno od rudého posuvu, který se má vykompenzovat modrým posuvem během návratu a dvojčata budou při setkání stejně stará.
• Další nesprávné řešení vychází z problematického zadání se zanedbaným „rychlým“ zrychlením. Cestující dvojče má při rychlé otočce absolvovat (téměř) nekonečné zrychlení, které má být hlavním důvodem dilatace času. Zrychlení dle obecné relativity skutečně ovlivňuje plynutí času, ale z upraveného zadání s dvojicí rovnoměrně se pohybujících raket vyplývá, že k dilataci dojde i bez zrychlování.
• Chybné je také tvrzení, že cestující dvojče bude při otočce pozorovat skok v pozemském čase. Relativní současnost je teoretický konstrukt, tak jako když pozemské dvojče na základě svých hodin počítá okamžik, kdy bratr dosáhne vzdálené hvězdy. Z grafu vysílání světelných signálů vyplývá, že k žádnému skoku při přímém pozorování nedojde, ale vlivem změny inerciální soustavy dojde k rozdílu v distribuci signálů v čase.

• PODOLSKÝ, Jiří; TROJÁNEK, Aleš. Paradox dvojčat jako pedagogický problém. Československý časopis pro fyziku. 2022, roč. 72, čís. 1, s. 28–36. Dostupné online. 

• Obrázky, zvuky či videa k tématu paradox dvojčat na Wikimedia Commons