Pythagorejská trojice

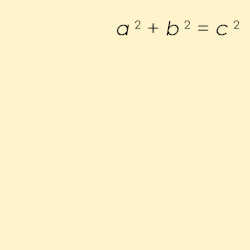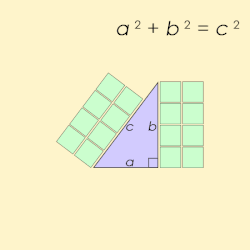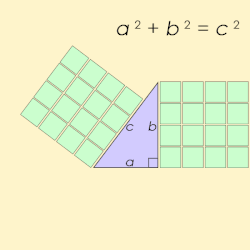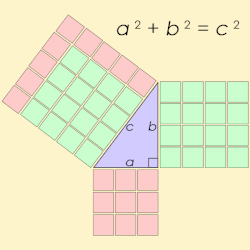
Pythagorejská trojice je v matematice trojice přirozených čísel ${\displaystyle (a,b,c)}$ (tj. celých kladných čísel), které lze využít jako velikosti stran pravoúhlého trojúhelníka. Tyto celočíselné kombinace byly využívány již ve starověku a jsou dones využívány v běžném životě (např. vyměření pravého úhlu na stavbě pomocí provázku s uzly ve stejných vzdálenostech, případně vyměření pravého úhlu svinovacím metrem v násobku jedné z Pythagorejských trojic).

Název pythagorejská trojice je odvozen od Pythagorovy věty, která definuje pro strany pravoúhlého trojúhelníka vztah: ${\displaystyle a^{2}+b^{2}=c^{2}}$

Pro čísla do 100 je celkem 16 základních Pythagorejských trojic:

• 3, 4, 5
• 5, 12, 13
• 8, 15, 17
• 7, 24, 25
• 20, 21, 29
• 12, 35, 37
• 9, 40, 41
• 28, 45, 53
• 11, 60, 61
• 16, 63, 65
• 33, 56, 65
• 48, 55, 73
• 13, 84, 85
• 36, 77, 85
• 39, 80, 89
• 65, 72, 97

Mezi Pythagorejské trojice patří také všechny násobky výše uvedených trojic. Například Pythagorejská trojice ${\displaystyle (6,8,10)}$ nebo ${\displaystyle (30,40,50)}$ není základní Pythagorejskou trojicí, protože je násobkem základní trojice ${\displaystyle (3,4,5)}$.

Generátorem pythagorejských trojic rozumíme trojici funkcí ${\displaystyle (a,b,c)=f(p_{1},p_{2},\ldots )}$, která parametrizuje nějakou množinu trojic. Dosazením konkrétních hodnot za parametry ${\displaystyle p_{j}}$ dostaneme (vygenerujeme) jednotlivé hodnoty čísel ${\displaystyle a,b,c\,\!}$ pythagorejské trojice. Ideální generátor je takový, který vygeneruje právě všechny základní trojice (tedy nikoliv jejich netriviální násobky).

Klasický generátor pythagorejských trojic čísel je funkce ${\displaystyle (a,b,c)=f(x,y)}$, kde ${\displaystyle x,y\in \mathbb {N} }$ a ${\displaystyle x>y\,\!}$, a

${\displaystyle a=2xy}$,

${\displaystyle b=x^{2}-y^{2}}$,

${\displaystyle c=x^{2}+y^{2}}$.

Tato funkce však generuje i netriviální násobky základních trojic.

Mohou existovat i jiné generátory pythagorejských trojic čísel, které pak mají specifické vlastnosti.

Zde uvedené generátory například dokáží vygenerovat všechny možné trojice pro definované podmínky, netriviální násobky základních jsou ale generátorem vynechány.

Pro vygenerování trojic, které splňují podmínku ${\displaystyle c-b=1}$, lze použít generátor

${\displaystyle a=2n+1}$,

${\displaystyle b=2n^{2}+2n}$,

${\displaystyle c=2n^{2}+2n+1}$.

V případě trojic, které splňují podmínku ${\displaystyle c-b=2\,\!}$, lze použít generátor

${\displaystyle a=4n}$,

${\displaystyle b=4n^{2}-1}$,

${\displaystyle c=4n^{2}+1}$.

• Velká Fermatova věta

• Obrázky, zvuky či videa k tématu Pythagorejská trojice na Wikimedia Commons
• Encyklopedické heslo Pythagorova čísla v Ottově slovníku naučném ve Wikizdrojích
• Metodika hledání pythagorejských trojic