Sedlový bod

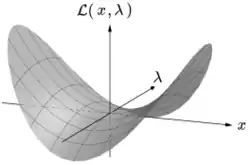
Sedlový bod Lagrangeovy funkce

Sedlový bod je v matematice bod na ploše grafu funkce, kde jsou všechny sklony (derivace) v na sebe kolmých směrech nulové (kritický bod), ale který není lokálním extrémem funkce.[1] Příkladem sedlového bodu je, když existuje kritický bod s relativním minimem podél jednoho osového směru (mezi vrcholy) a relativním maximem podél druhého na něj kolmého osového směru.

V teorii her je sedlový bod takový prvek matice hry, který je maximální ve svém sloupci a zároveň minimální ve svém řádku (nebo naopak), tj. označuje takovou dvojici strategií, kterou zastávají-li oba hráči, žádný z nich si změnou strategie nemůže polepšit.

Odkazy

Reference

V tomto článku byl použit překlad textu z článku Saddle point na anglické Wikipedii.

  1. ↑ CHIANG, Alpha C. Fundamental Methods of Mathematical Economics. 3rd. vyd. New York: McGraw-Hill, 1984. Dostupné online. ISBN 0-07-010813-7. S. 312. 

Související články

Externí odkazy

  • Obrázky, zvuky či videa k tématu sedlový bod na Wikimedia Commons
This article is issued from Wikipedie. The text is available under Creative Commons Attribution-Share Alike 4.0 unless otherwise noted. Additional terms may apply for the media files.