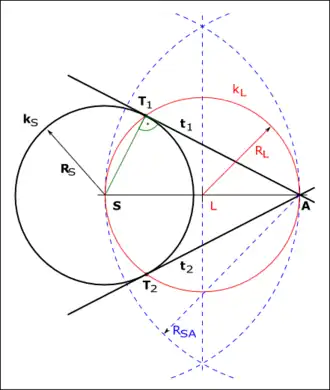
Tečna kružnice

Tečna kružnice je přímka, jež má s danou kružnicí právě jeden společný bod dotyku.

Nechť je dána kružnice ${\displaystyle k_{S}}$ se středem ${\displaystyle S}$ a poloměrem ${\displaystyle R_{S}}$ a bod ${\displaystyle A}$ vně této kružnice. Ukážeme konstrukci tečny ke kružnici, která prochází bodem ${\displaystyle A}$.

1. Body ${\displaystyle S}$ a ${\displaystyle A}$ spojme přímkou.
2. Zkonstruujme střed úsečky ${\displaystyle SA}$, který označíme ${\displaystyle L}$.
3. Narýsujme kružnici ${\displaystyle k_{L}}$ se středem v bodě ${\displaystyle L}$ o poloměru ${\displaystyle R_{L}}$, kde poloměr ${\displaystyle R_{L}}$ je roven velikosti úsečky ${\displaystyle LA}$ (a také ${\displaystyle LS}$).
4. V průniku kružnic ${\displaystyle k_{S}}$ a ${\displaystyle k_{L}}$ jsou body ${\displaystyle T_{1}}$ a ${\displaystyle T_{2}}$
5. Body ${\displaystyle T_{1}}$ a ${\displaystyle A}$ veďme přímku, která je tečnou ${\displaystyle t_{1}}$ ke kružnici ${\displaystyle k_{S}}$ v bodě ${\displaystyle T_{1}}$
6. Analogicky zkonstruujme tečnu ${\displaystyle t_{2}}$.
7. Thaletova věta říká, že úhel ${\displaystyle ST_{1}A}$ a ${\displaystyle ST_{2}A}$ je kolmý (90°), tedy je splněna podmínka tečny (jeden bod dotyku s kružnicí).

Je dána kružnice ${\displaystyle k}$ se středem v bodě ${\displaystyle S}$ a přímka ${\displaystyle p}$.

1. Sestrojíme kolmici ${\displaystyle q}$ na přímku ${\displaystyle p}$ tak, aby procházela bodem ${\displaystyle S.}$
2. Body, ve kterých se kružnice ${\displaystyle k}$ protne s přímkou ${\displaystyle q}$ označíme ${\displaystyle T}$ a ${\displaystyle T'.}$
3. Sestrojíme dvě kolmice (tečny) na přímku ${\displaystyle q}$ procházející body ${\displaystyle T}$ a ${\displaystyle T'}$ a označíme je ${\displaystyle t}$ a ${\displaystyle t'.}$

Tečna t ke kružnici k, se středem ${\displaystyle S\left[m;n\right]}$ a rovnicí:

${\displaystyle \left(x-m\right)^{2}+\left(y-n\right)^{2}=r^{2}}$,

v bodě ${\displaystyle T_{0}\left[x_{0};y_{0}\right]}$ kružnice je zapsána rovnicí:

${\displaystyle \left(x_{0}-m\right)\left(x-m\right)+\left(y_{0}-n\right)\left(y-n\right)=r^{2}}$

Dosazením a úpravou vyjde obecná rovnice poláry, tedy přímky procházející kružnicí v tečných bodech. Dosazením do rovnice kružnice získáme souřadnice tečných bodů.

• Kružnice
• Tečna
• Sečna