Schematická značka transformátoru využívajícího vzájemnou indukčnost pro přenos energie.Vzájemná indukčnost je fyzikální veličina , vyjadřující velikost vzájemné indukce dvou blízkých cívek . Popisuje vliv magnetického pole vyvolaného proudem procházejícím jednou cívkou na napětí indukované v druhé cívce. V závislosti na orientaci vinutí cívek se přičítá nebo odečítá od indukčnosti vlastní
Značení a výpočet
Značka :
M
{\displaystyle M}
Jednotka SI henry , značka
H
{\displaystyle \mathrm {H} }
Obecný vzorec:
L
Σ
=
L
±
M
{\displaystyle L_{\Sigma }=L\pm M}
Známe-li vlastní indukčnosti obou cívek a jejich vazbu, můžeme vzájemnou indukčnost spočítat jako
M
=
k
⋅
L
1
L
2
,
{\displaystyle M=k\cdot {\sqrt {L_{1}L_{2}}},}
kde
k
∈
⟨
0
,
1
⟩
{\displaystyle k\in \langle 0,1\rangle }
Protéká-li první cívkou proud
i
1
{\displaystyle i_{1}}
u
2
{\displaystyle u_{2}}
u
2
=
M
⋅
d
i
1
d
t
,
{\displaystyle u_{2}=M\cdot {\frac {\mathrm {d} i_{1}}{\mathrm {d} t}},}
u
1
=
M
⋅
d
i
2
d
t
.
{\displaystyle u_{1}=M\cdot {\frac {\mathrm {d} i_{2}}{\mathrm {d} t}}.}
Protéká-li proud oběma cívkami, výsledné napětí na cívkách se stanoví jako
u
1
=
L
1
⋅
d
i
1
d
t
±
M
⋅
d
i
2
d
t
,
{\displaystyle u_{1}=L_{1}\cdot {\frac {\mathrm {d} i_{1}}{\mathrm {d} t}}\pm M\cdot {\frac {\mathrm {d} i_{2}}{\mathrm {d} t}},}
u
2
=
L
2
⋅
d
i
2
d
t
±
M
⋅
d
i
1
d
t
.
{\displaystyle u_{2}=L_{2}\cdot {\frac {\mathrm {d} i_{2}}{\mathrm {d} t}}\pm M\cdot {\frac {\mathrm {d} i_{1}}{\mathrm {d} t}}.}
Vlastnosti
Při souhlasném zapojení (sériovém či paralelním při souhlasné orientaci vinutí) se vzájemná indukčnost přičítá.
Při nesouhlasném zapojení (antisériovém či antiparalelním při opačné orientaci vinutí) se vzájemná indukčnost odečítá.
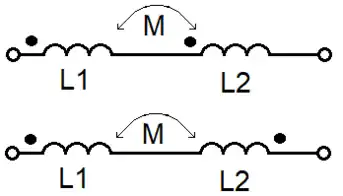
Zapojení cívek
Sériové (nahoře) a antisériové (dole) spojení dvou cívek – tečka značí začátek vinutí
Sériové řazení cívek
Při sériovém řazení platí podle Kirchhoffových zákonů :
i
1
=
i
2
=
i
;
u
1
+
u
2
=
u
,
{\displaystyle i_{1}=i_{2}=i;u_{1}+u_{2}=u,}
u
1
=
(
L
1
±
M
)
⋅
d
i
d
t
,
{\displaystyle u_{1}=(L_{1}\pm M)\cdot {\frac {\mathrm {d} i}{\mathrm {d} t}},}
u
1
=
(
L
2
±
M
)
⋅
d
i
d
t
,
{\displaystyle u_{1}=(L_{2}\pm M)\cdot {\frac {\mathrm {d} i}{\mathrm {d} t}},}
u
=
(
L
1
+
L
2
±
2
M
)
⋅
d
i
d
t
,
{\displaystyle u=(L_{1}+L_{2}\pm 2M)\cdot {\frac {\mathrm {d} i}{\mathrm {d} t}},}
z čehož lze následně odvodit
L
Σ
=
L
1
+
L
2
±
2
M
.
{\displaystyle L_{\Sigma }=L_{1}+L_{2}\pm 2M.}
Pokud bychom uvažovali dvě cívky, které by byly navinuté na stejném jádře stejným počtem závitů ale každá opačným směrem, pak by platilo:
L
2
=
L
1
{\displaystyle L_{2}=L_{1}}
k
=
1
,
{\displaystyle k=1,}
M
=
k
⋅
L
1
L
2
=
L
1
,
{\displaystyle M=k\cdot {\sqrt {L_{1}L_{2}}}=L_{1},}
L
=
L
1
+
L
2
−
2
M
=
L
1
+
L
1
−
2
L
1
=
0
,
{\displaystyle L=L_{1}+L_{2}-2M=L_{1}+L_{1}-2L_{1}=0,}
v takovém případě by byl vliv indukčnosti zcela potlačen, čehož využívá například tzv. bifilární vinutí .
Paralelní řazení cívek
Při paralelním zapojení platí podle Kirchhoffových zákonů :
i
1
+
i
2
=
i
;
u
1
=
u
2
=
u
,
{\displaystyle i_{1}+i_{2}=i;u_{1}=u_{2}=u,}
u
1
=
L
1
d
i
1
d
t
±
M
d
i
2
d
t
,
{\displaystyle u_{1}=L_{1}{\frac {\mathrm {d} i_{1}}{\mathrm {d} t}}\pm M{\frac {\mathrm {d} i_{2}}{\mathrm {d} t}},}
u
2
=
L
2
d
i
2
d
t
±
M
d
i
1
d
t
,
{\displaystyle u_{2}=L_{2}{\frac {\mathrm {d} i_{2}}{\mathrm {d} t}}\pm M{\frac {\mathrm {d} i_{1}}{\mathrm {d} t}},}
z čehož lze následně odvodit:
L
Σ
=
1
1
L
1
±
M
+
1
L
2
±
M
.
{\displaystyle L_{\Sigma }={\frac {1}{{\frac {1}{L_{1}\pm M}}+{\frac {1}{L_{2}\pm M}}}}.}
[ 1]
Dvě cívky svázané transformátorovou vazbou a jejich ekvivalentní obvod Pokud jsou cívky od sebe galvanicky odděleny a ovlivňují se pouze magnetickými poli, hovoříme o transformátorové vazbě. Takovéto uspořádání dvou cívek lze nahradit ekvivalentním obvodem ze tří cívek, z nichž jedna reprezentuje vzájemnou indukčnost. Tento model je platný, pokud:[ 2]
L
A
=
L
1
−
M
,
{\displaystyle L_{\mathrm {A} }=L_{1}-M,}
L
B
=
L
2
−
M
,
{\displaystyle L_{\mathrm {B} }=L_{2}-M,}
L
C
=
M
.
{\displaystyle L_{\mathrm {C} }=M.}
Odkazy
Reference
Související články